
if the ray does not pass the interface between the two materials.Īll details of GLSL for OpenGL are specified in the “OpenGL Shading Language 4.10.6 Specification” available at the Khronos OpenGL web site.
MULTIPLY A SCALAR WITH VECTOR CODE CODE
TYPE is any of: float, vec2, vec3 and vec4 (only one of them per line).įloat d = 1.0 - r * r * ( 1.0 - dot ( n, i ) * dot ( n, i )) if ( d < 0.0 ) return TYPE ( 0.0 ) // total internal reflection return r * i - ( r * dot ( n, i ) + sqrt ( d )) * n Īs the code shows, the function returns a vector of length 0 in the case of total internal reflection (see the entry in Wikipedia), i.e. The following functions are particular useful for vector operations. There are more built-in functions, which also work component-wise but are less useful for vectors, e.g., abs, sign, floor, ceil, fract, mod, step, smoothstep, sqrt, inversesqrt, pow, exp, exp2, log, log2, radians (converts degrees to radians), degrees (converts radians to degrees), sin, cos, tan, asin, acos, atan (with one argument and with two arguments for signed numerator and signed denominator), lessThan, lessThanEqual, greaterThan, greaterThanEqual, equal, notEqual, and not. TYPE min ( TYPE a, TYPE b ) // returns a if a b, b otherwise TYPE max ( TYPE a, float b ) // returns a if a > b, b otherwise TYPE clamp ( TYPE a, TYPE minVal, TYPE maxVal ) // = min(max(a, minVal), maxVal) TYPE clamp ( TYPE a, float minVal, float maxVal ) // = min(max(a, minVal), maxVal) TYPE mix ( TYPE a, TYPE b, TYPE wb ) // = a * (TYPE(1.0) - wb) + b * wb TYPE mix ( TYPE a, TYPE b, float wb ) // = a * TYPE(1.0 - wb) + b * TYPE(wb) Thus, multiplying a vector from the left to a matrix corresponds to multiplying it from the right to the transposed matrix: Note in particular that a * b represents a component-wise product of two vectors, which is not often seen in linear algebra.įor matrices, these operators also work component-wise, except for the *-operator, which represents a matrix-matrix product, e.g.:Ī B =

To define default precisions for all floating-point variables, you should use the precision command, for example: from -2.0 to 2.0), thus, lowp is most useful for colors but usually not for positions. Also note that the range of lowp variables can be very limited (e.g.
MULTIPLY A SCALAR WITH VECTOR CODE DRIVER
Note that it is up to the compiler and driver to decide which precision is actually used the precision qualifiers are only suggestions by the programmer. (There are only a few exceptions to this, for example accessing individual elements of a lowp vector can be slower than for a mediump vector because it requires additional decoding.)

Thus, for best performance you should use the lowest precision that still gives satisfactory results. The idea is that lowp variables require less computation time and less storage (and therefore also less bandwidth) than mediump variables, and mediump variables require less time than highp variables.

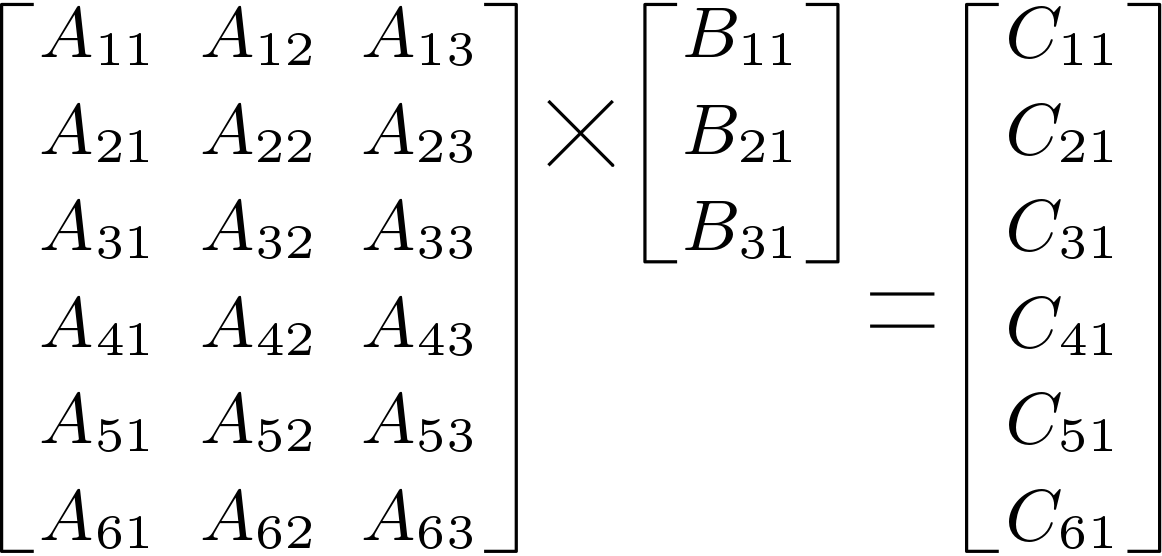
Lowp vec4 color // for colors, lowp is usually fine mediump vec4 position // for positions and texture coordinates, mediump is usually ok highp vec4 astronomical_position // for some positions and time, highp is necessary //(precision of time measurement decreases over time //and things get jumpy if they rely on absolute time since start of the application)


 0 kommentar(er)
0 kommentar(er)
